論理回路

發表於 分類於
文章字數： 2.9k 所需閱讀時間 ≈ 5 分鐘

這將是我的論理回路一週筆記，希望通過這個筆記可以讓我更深入的理解這本書的知識，寫完報告以及考出一個好成績（PS:我不想這門課修兩次…）。
この授業ではデジタル電子回路（大類重範）を参照する。

第一週

第一週名詞解析

  1. アナログ信号：(Analogue)連続した電気信号。
  2. デジタル信号：(Digital)不連続した電気信号。
  3. A/D変換：Analogue信号からDigital信号へ変換する方法。詳しいは標本化、量子化と符号化の三つの手順で変換すること。
  4. 標本化(サンプリング)：(Sampling):Analogue信号を一定な時間TをSampling周期で離散な信号へ変換すること。
  5. 量子化：標本化した離散な信号をあらかじめ決められたレベルに変換する操作。
  6. 量子化誤差：量子化より標本化と生じた誤差は量子化誤差という。

トランジスタ(Transistor)

この章ではTransistorの増幅作用とスイッチング作用を紹介する。(p10~p14参照)
電晶體主要作用為透過微小的電流來達到開關Switch的功效，而電晶體的增幅作用則可以
讓類比電路在不失真的狀況下穩定的輸出。（這個部分的圖表我還不是很清楚xd）

章末習題

  1. アナログ信号からデジタル信号に変換するとき、どのような変換過程を通して行われるか？
    標本化、量子化と符号化を通して行われるとA/D変換する。
  2. ストレートバイナリとオフセットバイナリの関連について述べよ。
    オフセットバイナリでは二の補数を使って、ストレートバイナリと同じ数の分解能であるが、負数を含めて表示することができる。
  3. コレクタ遮断電流ICBOI_{CBO}とトランジスタが飽和したときの電圧VCE(S)V_{CE(S)}とは何か。またこれらの値を無視した時、トランジスタのスイッチング作用について説明せよ。
    (ベース接地の)コレクタ遮断電流ICBOI_{CBO}とは、エミッタをオープンにして、コレクターベース間のPN接合に逆電圧を印可した時の漏れ電流です。まだトランジスタが飽和したときの電圧とはトランジスタがベース電流を増加させてもコレクタ電流は飽和して増加しなくなる時はトランジスタが飽和という。飽和している時のコレクタ・エミッタ間電圧はVCE(S)V_{CE(S)}tと表じしている。

第二週

第二週重點複習

本章節著重於2進位、8進位、16進位、以及2進位的1的補數2的補數、BCD Code 跟Gray Code的計算方式。（考試的話只需熟悉計算方法，使用章末習題練習，以能快速計算為目標。）

  1. 各種進位制都很簡單，把10進位做直式除法換算即可算出2,8,16進位的值。其中8進位的編碼方式為3個bit的2進位值做換算,16進位則為4個bit的2進位換算。若演算數字大於0則從MSB加到LSB（下到上）,小於0則相反（上到下）
  2. BCD Code 則為把10進位的概念帶入2進位制。詳情見下圖
    由圖可見， BCD是把10的進位用2的進位來計算，每4個bit最大為9。若演算時超過10~18之間，則需添加6 (0110)2(0110)_2來導正結果。
  3. Gray Code 則是為了在計算時用最少的值的變化來減少差錯，每+1+ 1 一次，也只變化一個bit為其最大的優點，見下圖為2進位變換Gray Code的計算方式。
  4. 1的補數、2的補數則是以2進位制的負數運算
    1. 1的補數： (2n−1)10−B2(2^n - 1)_10 -B_2
      運算時，若有進位，則為正，並於LSB加1
    2. 2的補數： (2n)10−B2(2^n)_10 - B_2
      運算時，若有進位，則為正。

第三週

本章節為本書的重點章節，內容在描述透過信號0,1的組合所組成的基礎論理回路（以MILitary Standard Specification方式標記）。而為了方便論理代數（Bool Algebra）的計算，將會使用以下工具來表達以及計算論理式、真理表、論理式的展開標準形、Kernal圖。

第三週重點複習

基礎論理回路以及記號

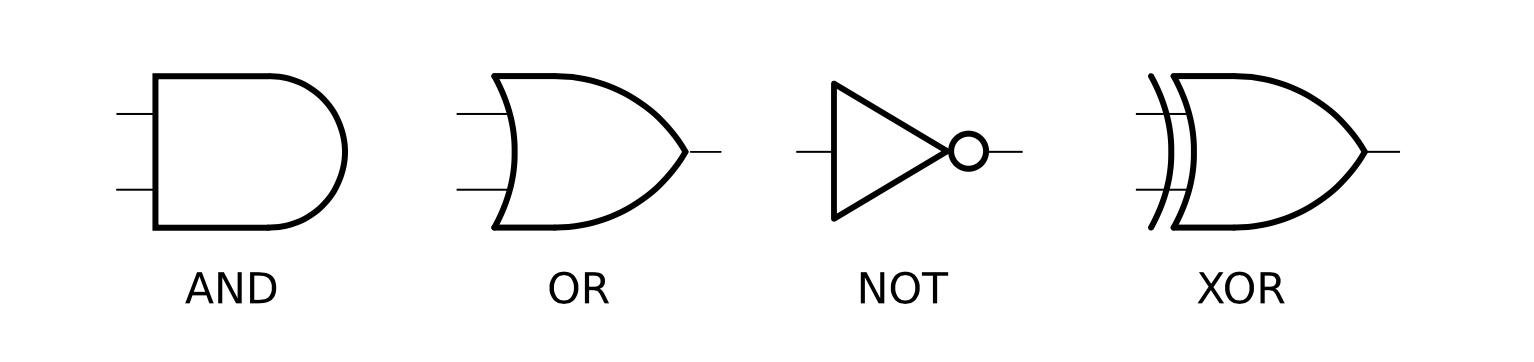
  1. OR回路 X=A+BX = A +B
  2. AND回路X=A∗BX = A * B
  3. NOT回路X=AˉX = \bar{A}
  4. NAND回路X=A⋅B‾X = \overline{A \cdot B}
  5. EXOR回路Aˉ⋅B+A⋅Bˉ\bar{A} \cdot B + A \cdot \bar{B}

正論理與負論理

正論理：設高電位H為1低電位L為0是為正論理。
負論理：設高電位H為0低電位L為1是為正論理。

由正負論理的真理值來看，我們可以得出正論理AND回路的輸出結果與負論理的OR回路相同。
正負論理可以幫助我們在複雜的電路圖中判斷以及方便計算。比如使用狄摩根公式等等。

論理代數(Boolean Algebra)

好用的公式（？

  1. 變數消去： 1+A=11+A = 1 , A+A‾=1A + \overline A = 1 , A⋅A‾=0A \cdot \overline A = 0
  2. 同一變數消去：A+A=AA + A = A, A⋅A=AA \cdot A =A
  3. 變數壓縮：A+A⋅B=AA + A \cdot B = A , A(A+B)=AA(A+B) = A , (A+B)(A+B‾)=A(A+B)(A+\overline B) = A
  4. 分配則：A+B⋅C=(A+B)(A+C)A + B \cdot C = (A+B)(A+C)
  5. 內外分配：(A+B)(A‾+C)=A‾⋅B+A⋅C(A+B)(\overline A + C) = \overline A \cdot B + A \cdot C
  6. 狄摩根定律：A+B+C⋯‾=Aˉ⋅Bˉ⋅Cˉ⋯\overline{A + B + C \cdots} = \bar{A} \cdot \bar{B} \cdot \bar{C} \cdots
    A⋅B⋅C⋯‾=Aˉ+Bˉ+Cˉ⋯\overline{A \cdot B \cdot C \cdots} = \bar{A} + \bar{B} + \bar{C} \cdots

根據這些公式可以幫助我們快速計算論理回路的電路值。

論理回路的標準展開式

加法標準型

變換手順

  1. 選出真理值表結果為"1"的部分。
  2. 將變數挑出，變數為1的部分為正,變數為0的部分為負。
  3. 將所有的變數的論理積累總。
乘法標準型

變換手順

  1. 選出真理值表結果為"0"的部分。
  2. 將變數挑出，變數為0的部分為正,變數為1的部分為負。
  3. 將所有的變數的論理和累乘。

簡化論理式

  1. 利用公式簡化（每次都搞好久orz
  2. 利用kernal圖簡化
    變換手順
    1. 以加法標準型展開
    2. 將每個項目計入圖中
    3. 圈起來
    4. 讀取重複部分的論理和

本週總結

論理式對於簡化以及計算論理電路帶來極高的方便性，在此重述一次電路分析的過程。（詳見章末習題第3.7題）
變換手順

  1. 寫出希望得出結果的真理值表
  2. 透過真理表分析出每一個結果所對應的變數值並以標準型來得出論理式並簡化
  3. 透過簡化的論理是來試著畫出基礎電路圖組合